miércoles, 31 de octubre de 2018
lunes, 8 de octubre de 2018
FUNCIÓN RACIONAL
TEMAS DE CONSULTA E INTERÉS DEL TEMA
En este artículo te voy a explicar brevemente lo que son las funciones racionales y te mostraré unas funciones racionales ejemplos para que las entiendas mejor. 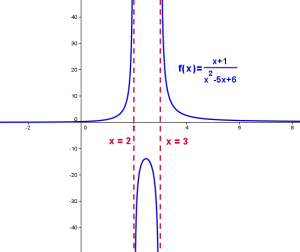 Una función es racional si:
Una función es racional si: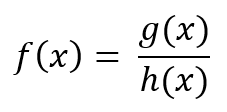 en donde g(x) y h(x) son polinomios. El dominio de la función serán todos los números reales con excepción los números en los cuales se hace cero el denominador.
en donde g(x) y h(x) son polinomios. El dominio de la función serán todos los números reales con excepción los números en los cuales se hace cero el denominador.
 Una función es racional si:
Una función es racional si: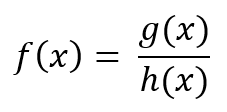 en donde g(x) y h(x) son polinomios. El dominio de la función serán todos los números reales con excepción los números en los cuales se hace cero el denominador.
en donde g(x) y h(x) son polinomios. El dominio de la función serán todos los números reales con excepción los números en los cuales se hace cero el denominador.
Por ejemplo en una función f (x ) = 1 / x – 2, el dominio es toda x excepto x =2.
Cuando se hace la gráfica de una función racional es importante saber:
- Qué se puede decir de los valores de la función cuando x se acerca a un cero del denominador?
- Qué se puede decir de los valores de la función cuando x es grande y positiva o negativa?
Asíntota vertical
La recta x = a es una asíntota vertical de la gráfica de una función si f (x) –> ∞ o f (x) –> -∞ cuando xtiende a a.
Asíntota horizontal
La recta y = c es una asíntota horizontal de la gráfica de una función si f (x) –> c cuando x –> ∞ o cuando x –> -∞
https://matemovil.com/funcion-racional-ejercicios-resueltos/miércoles, 26 de septiembre de 2018
DEFINICIÓN DEPROGRAMACIÓN LINEAL
Se conoce como programación lineal a la técnica de la matemática que permite la optimización de una función objetivo a través de la aplicación de diversas restricciones a sus variables. Se trata de un modelo compuesto, por lo tanto, por una función objetivo y sus restricciones, constituyéndose todos estos componentes como funciones lineales en las variables en cuestión.
Fuente: https://definicion.de/programacion-lineal/
miércoles, 12 de septiembre de 2018
FUNCIÓN INYECTIVA
Se cumple que para todo elemento del conjunto llegada existe
como máximo un elemento en el conjunto de partida.
FUNCIÓN SOBREYECTIVA
Se cumple que para todo elemento del conjunto llegada existe
por lo menos un elemento en el conjunto de partida.
FUNCIÓN BIYECTIVA
Toda función es biyectiva si es inyectiva y sobreyectiva a
la vez
FUENTE DE IMAGEN: https://www.youtube.com/watch?v=ApRLgmX_iN0
Suscribirse a:
Comentarios (Atom)


